Technical Description of 3D Scanning
3D scanners are devices used to capture physical dimensions from objects and scenes for computer aided use. Typical applications of 3D scanners include, Computer Aided Design (CAD), Quality Inspection, Manufacturing, and many application specific uses such as 3D digital impressions in dentistry and hearing aids.
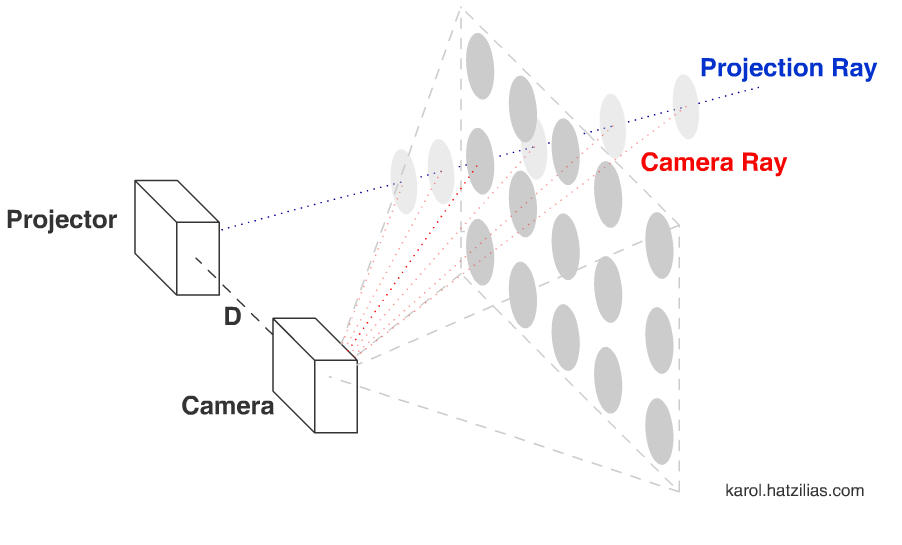
3D scanners typically use simple triangulation. I put together a couple images to help explain this. In this explanation I show a single camera and single projector 3D scanner. The projector is a known distance, D away from the camera. The projector is projecting a series of circles. Each circle lies upon a projection ray. If you ignore lens distortion the center of these circles will always fall on the same ray, independent of distance from the projector.
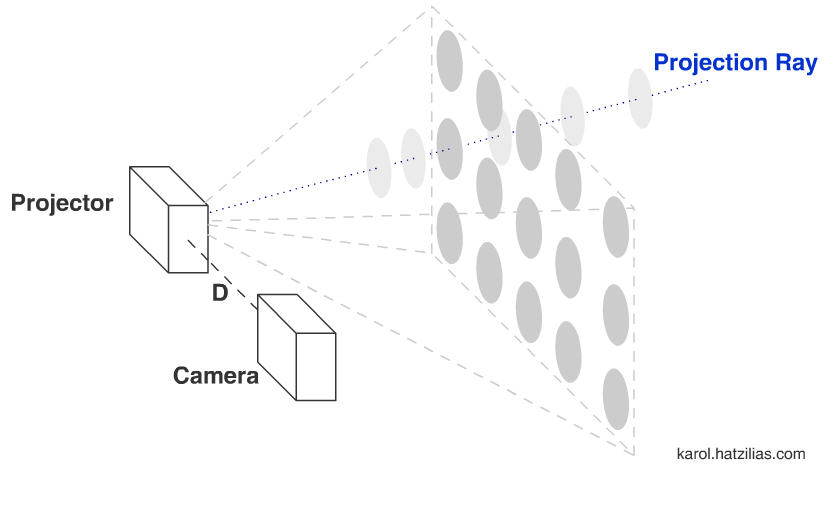
To illustrate the triangulation that takes place within a 3D scanner I have included a top down view of the same setup. The angle a for each projection ray is precisely known because we know the optics of the projector. In other words, the amount the projection grows or shrinks when the distance to the projector changes remains constant for each projector. You may have experienced this with an overhead projector, to make the image bigger, move the projector back.
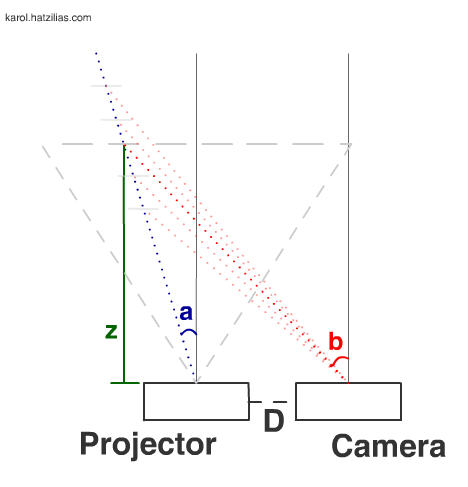
A camera is similar, as you move the camera farther away from an object it gets smaller, as you get closer to an object it appears bigger in the image. It is possible to very precisely calculate the amount the projection or image will grow or shrink using a process called lens calibration. Therefore, when I say 'we know the optics of the projector' I mean we've very precisely calibrated it and we know the angle of each projection ray.
If we take a picture of the projection using the camera in the illustration, we can use image processing to identify the circles within the image. We can draw a ray from the center of the camera through each circle. In the illustrations you can see as the projected circles get farther the angle of the camera ray, b, changes. By analyzing the angles a and b, we can determine the distance Z to the circle.